Notes from a lecture conference, introduced some progress of machine learning solving combinatorial optimization problems, especially combinatorial optimization problems on graphs, including autoregression-based methods and non-autoregression-based methods.

Machine learning solution of combinatorial optimization problems ¹

CO and ML4CO

Combinatorial optimization

• Combinatorial optimization is to find the optimal arrangement, grouping, order or screening of discrete events through the study of mathematical methods. The problem can be described mathematically as:

  \[min \quad f(x) \\ s.t. \quad g(x) \geq 0 \\ \qquad\quad x \in D\]

  Where $D$ is a set of finite points (the domain), $f$ is the objective function, and \(F= \{ x \ \vert \ x \in D, \ g(x) \geq 0 \}\) is the feasible region.

• 0-1 knapsack problem, traveling salesman problem, minimum vertex cover problem, maximum cut problem and so on.

Machine learning for combinatorial optimization

Optimization algorithms

• Mathematical Optimization algorithms - Exact algorithms (Exponential time)
  • Branch and bound, Branch and price, Branch and cut, Cutting plane, Lagrangian relaxation
• Heuristic algorithms (Polynomial time)
  • Approximation algorithm, Greedy algorithm, Rule-based construction algorithm
• Meta heuristic algorithms (Polynomial time)
  • Genetic algorithm, Ant colony algorithm, Tabu search, Simulated annealing
• Machine learning methods (Polynomial time)
  • Supervised learning, Reinforcement learning, Graph neural networks

Combinatorial Optimization Solvers

• Commercial Solvers
  • Gurobi, CPLEX, Matlab, Lingo, CMIP
• Open Source Solvers
  • SCIP, LP_Solve, CBC, GLPK, MOSEK

Past and Now

• Traditional solvers: Moderate scale, relatively stable, classical problem, theoretical guarantee
• Machine learning: Super large scale, real-time change, complex system, weak optimization

Machine learning paradigms for solving CO problems

• End-to-end solver $\rightarrow$ autoregressive/non-autoregressive $\rightarrow$ Learning heuristics
• Local improvement solution $\rightarrow$ ML + Traditional operations algorithm $\rightarrow$ Improving OR Solvers

Combinatorial optimization problem solving on the graph

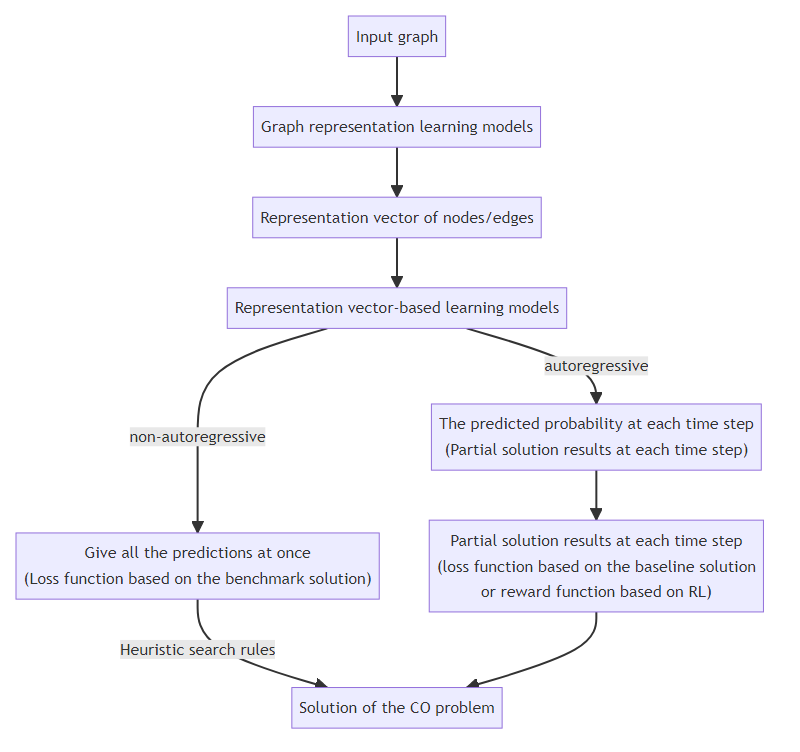
Non-autoregressive algorithms

• Supervised learning + Tree search + Graph theory tricks
• Li Z, Chen Q, Koltun V. Combinatorial optimization with graph convolutional networks and guided tree search[J]. Advances in neural information processing systems, 2018, 31.

Autoregressive algorithms

• S2V - DQN
  • Khalil E, Dai H, Zhang Y, et al. Learning combinatorial optimization algorithms over graphs[J]. Advances in neural information processing systems, 2017, 30.
• FINDER
  • Fan C, Zeng L, Sun Y, et al. Finding key players in complex networks through deep reinforcement learning[J]. Nature machine intelligence, 2020, 2(6): 317-324.
• DIRAC
  • Fan C, Shen M, Nussinov Z, et al. Searching for spin glass ground states through deep reinforcement learning[J]. Nature Communications, 2023, 14(1): 725.
  • Lucas A. Ising formulations of many NP problems[J]. Frontiers in physics, 2014, 2: 5.
  • Barrett T, Clements W, Foerster J, et al. Exploratory combinatorial optimization with reinforcement learning[C]//Proceedings of the AAAI conference on artificial intelligence. 2020, 34(04): 3243-3250.
  • Yao F, Cai R, Wang H. Reversible action design for combinatorial optimization with reinforcement learning[J]. arXiv preprint arXiv:2102.07210, 2021.

Summary of autoregressive algorithms

Graph Representation Learning + Reinforcement Learning

• Pros
  • The model generalizes well
  • The model works well
  • It has some interpretability
• Cons
  • Model design and learning are difficult
  • Implementation is difficult

Some interesting research points

1. How to combine with exact algorithms?
   • Nair V, Bartunov S, Gimeno F, et al. Solving mixed integer programs using neural networks[J]. arXiv preprint arXiv:2012.13349, 2020.
2. How to combine with heuristics?
   • Mills K, Ronagh P, Tamblyn I. Finding the ground state of spin Hamiltonians with reinforcement learning[J]. Nature Machine Intelligence, 2020, 2(9): 509-517.
3. How to improve generalization on large instances?
   • Fu Z H, Qiu K B, Zha H. Generalize a small pre-trained model to arbitrarily large TSP instances[C]//Proceedings of the AAAI conference on artificial intelligence. 2021, 35(8): 7474-7482.
4. How do you handle complex constraints?
   • Donti P L, Rolnick D, Kolter J Z. DC3: A learning method for optimization with hard constraints[J]. arXiv preprint arXiv:2104.12225, 2021.
5. How to combine with mature solvers?
   • Pogančić M V, Paulus A, Musil V, et al. Differentiation of blackbox combinatorial solvers[C]//International Conference on Learning Representations. 2019.
6. How do you handle raw inputs that are more natural?
   • ChatGPT understands natural language problem requirements, models them automatically, and invokes a solver to solve them.